This page is an introduction to basic concepts used in thermodynamics and gas dynamics.

Ideal gas law

The ideal gas law sets a relationship between pressure ( p ), density ( ρ ) and temperature ( T ) of a gas at any time during a process:

p = ρRT

(1)

Where R is the specific gas constant. For air, R = 287 J/kg/K.

Specific heat capacity

Specific heat capacity is introduced here as the concept will come back often to evaluate work and addition of heat.

Specific heat capacity is the amount of heat required to change temperature of one kilogram of a substance by one degree.

Since enthalpy of a fluid is a function of its temperature and pressure, the temperature dependence of the enthalpy can be estimated by measuring the rise in temperature caused by the flow of heat at constant pressure. The constant-pressure heat capacity - C_p - is a measure of the change in enthalpy at a particular temperature.

Similarly, the internal energy is a function of temperature and specific volume. The constant volume heat capacity - C_v - is a measure of the change in internal energy at a particular temperature and constant volume.

The specific heat capacity represents the amount of energy required to raise 1 kg by 1°C, and can be thought of as the ability of a substance to absorb heat.

An interesting relationship between the two specific heats is the following:

Cp − Cv = R

(2)

Where R is the specific gas constant. For air, R = 287 J/kg/K.

Ratio of specific heats

The ratio of specific heats (γ) is defined as:

γ = Cp Cv

(3)

For air, γ = 1.4. This ratio varies with temperature. Mixing equations (2) and (3), we get the following relationships:

Cp = γR γ − 1	(4a)
Cv = R γ − 1	(4b)

Functions of ratio of specific heats

The following is a shorthand notation as presented in Design and simulation of Four-Stroke Engines, 1999, p. 160-161 by Gordon P. Blair.

Various functions of ratio of specific heats, which are useful as shorthand notation in many thermodynamics and gas dynamics equations, are given below. The logic of the notation for G is that the value of G₅ for air is 5, G₇ for air is 7, etc.

G3 = 4 − 2γ γ − 1 = 3 for air, where γ = 1.4

G4 = 3 − γ γ − 1 = 4 for air, where γ = 1.4

G5 = 2 γ − 1 = 5 for air, where γ = 1.4

G6 = γ + 1 γ − 1 = 6 for air, where γ = 1.4

G7 = 2γ γ − 1 = 7 for air, where γ = 1.4

G17 = γ − 1 2γ = 1 ⁄ 7   for air, where γ = 1.4

G72 = γ γ − 1 = 7 ⁄ 2   for air, where γ = 1.4

G52 = 1 γ − 1 = 5 ⁄ 2   for air, where γ = 1.4

G67 = γ + 1 2γ = 6 ⁄ 7   for air, where γ = 1.4

This useful notation simplifies analysis in gas dynamics, particularly because the equations are additive or subtractive with numbers, thus:

For example,

G4 = G5 − 1 = 2 γ − 1 − 1 = 2 − γ + 1 γ − 1 = 3 − γ γ − 1

Or

G7 = G5 + 2 or G3 = G5 − 2 or G6 = G3 + 3

However, it should be noted in applications of such functions that they are generally neither additive nor operable, thus:

G7 ≠ G4 + G3 and G3 ≠ G6 ⁄ 2

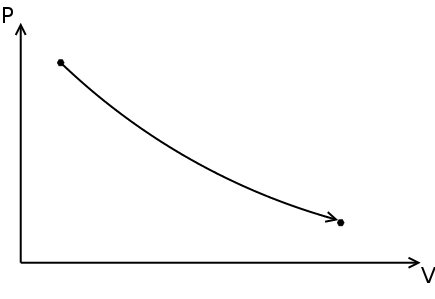
Polytropic process

A succession of polytropic processes can model the compression, combustion and expansion processes. The relationship between pressure ( p ) and density ( ρ ) for a polytropic process going from its initial state ( i ) to its final state ( f ) is:

pi ρin  =  pf ρfn

(5)

The value of n is the polytropic index and depends on the process. The specific work done for a polytropic process is:

wb  =  pf ⁄ ρf  −  pi ⁄ ρi 1 − n

(6a)

ws  =  n 1 − n ( pf ⁄ ρf  −  pi ⁄ ρi )

(6b)

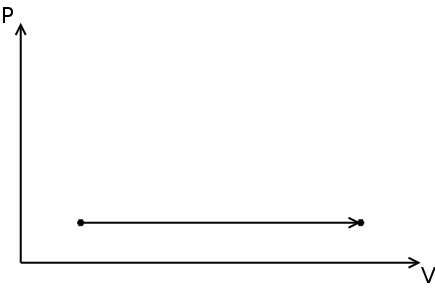
Where w_b is the specific boundary work (see graph & math representation) and w_s is the specific shaft work (see graph & math representation).

Boundary work is the work done by the expansion of gas, i.e. a variation of a volume (a moving piston inside a cylinder for example).

Shaft work is any other work that is not boundary work, i.e. where there is no variation of a volume (a turbine spinning inside a fixed housing for example).

Three basic processes can be identified, depending on the value of n :

**Note: If n = γ, then with equations (1) and (4b), specific boundary work is also −C_v( T_f − T_i ).

**Note: If n = γ, then with equations (1) and (4a), specific shaft work is also −C_p( T_f − T_i ).